An option's delta is a sensitivity measure used to evaluate an option derivative instrument.
Explanation-1: An option's delta is a rate of change in the price of an option with respect to a change in the price of the underlying asset, other factors being constant.
Explanation-2: An option's delta is an amount by which the price of an option is expected to change with respect to a $1 change in the price of the underlying asset, other factors being constant.
As per the explanations,
Option Delta = Δ in Option Price / Δ in Underlying Price
Example:
A 1-Day price movement is as follows:
The Strike Price is $1490.00
Underlying Price changes from $1488.05 to $1498.05
Call Option Premium changes from $8.72 to $14.34
Put Option Premium changes from $10.18 to $5.80
Therefore, using the risk sensitivity approach,
delta of a call option = ( Ct - Ct-1 ) / ( St - St-1 ) = ( $14.34 - $8.72 ) / ( $1498.05 - $1488.05 ) = 0.5620 represents that the price of a call option is expected to change by $0.5620 for every $1 change in the price of an underlying asset.
delta of a put option = ( Pt - Pt-1 ) / ( St - St-1 ) = ( $5.80 - $10.18 ) / ( $1498.05 - $1488.05 ) = -0.4380 represents that the price of a put option is expected to change by -$0.4380 for every $1 change in the price of an underlying asset.
There is a true relationship between the delta of a call option and the delta of a put option!
It is observed that the sum of absolute values of the delta of a call and a put is equal to 1. This relation is prevailing due to the Put-Call Parity theory which states that a protective put is equivalent to a fiduciary call, and therefore, a combination of a long call and a short put is equivalent to a long forward whose delta is equal to 1.
delta of a put option = delta of a call option - 1
For example,
If the delta of a call option is 0.5620, the delta of a put option is 0.5620 - 1 = -0.4380
It means, that if the price of the underlying asset increases by $1, the price of a call option is expected to increase by $0.5620 and that of a put option to decrease by $0.4380.
Simple right? -- not actually!
This relationship will hold good only if the underlying is a non-dividend or non-coupon-paying asset.
Option Delta: An Estimation Tool or A Risk Sensitivity?
'delta' sensitivity is important because it helps, (1). traders estimating the movement in the price of an option for any change in the price of the underlying asset. (2). risk managers to gauge the directional risk and being the most crucial risk attribute for analysis though it explains the first-order risk only.
The important point to note here is that the option risk sensitivities are in terms of a unit change in one single risk factor, while keeping other risk factors constant, unlike elasticity (stated in terms of percentage change in one factor) or simulation (simultaneous change in multiple risk factors).
Estimating the Price Movements using Pricing Formula
As discussed, traders use the option's delta to predict movements in the option's price based on the movements in the price of an underlying asset.
Mathematically speaking, if the price of an underlying asset increases, the option's delta of both call and put options increases too. However, the price of the call option increases, and that of the put option decreases. Similarly, if the price of an underlying asset decreases, the delta of both the call option and put option decreases too. However, the price of the call option decreases, and that of the put option increases.
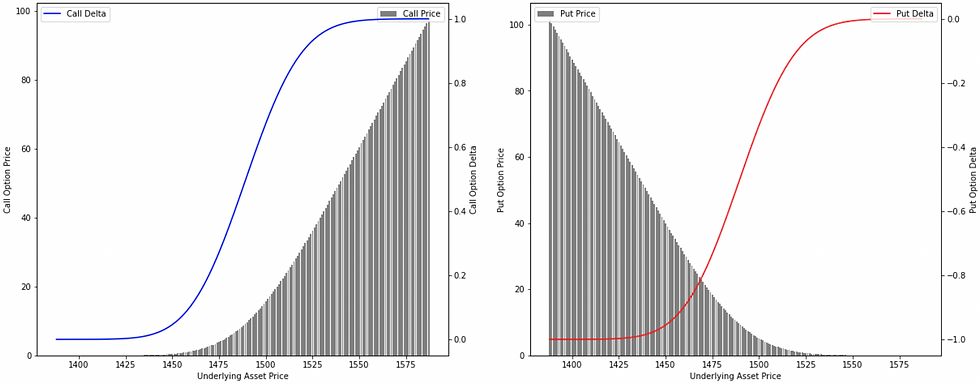
And because of this relationship, the delta of a call option always remains positive (it will range between 0 and 1, representing a positive relationship with the underlying) and the delta of a put option always remains negative (ranging between -1 to 0, representing a negative relationship with the underlying). This ranging variable (i.e. option's delta) may change depending upon the moneyness of an option as far as we look into the direction of the underlying asset. However, it may also change due to the change in the volatility and time-decay, but that is the next topic of our financial book.
The formula that has been stated above with an example is a sensitivity-based formula that strictly goes with explanations 1 and 2. However, professional traders determine the price of an option using some sophisticated models that often resemble the Black-Scholes-Merton (BSM) model. This model provides a mathematical function to estimate the theoretical price of an option by considering market risk factors.
Explanation-3: An option's delta is the probability that determines the expected payoff in case the option expires in the money.
As per the pricing function provided by the Black-Scholes-Merton (BSM) model,
C(0) = St * N(d1) - K*e^-rt * N(d2)
Here, N(d1) is the probability that helps in determining the expected payoff in case the option is getting exercised (or expires in the money). As per explanation 3, N(d1) is called the option's delta. The formula to arrive at this is actually provided by Black and Scholes in their pricing model.
N(d1) = [ (LN(St/K) + (r-q+σ^2/2)*T) / σ*√T ] from the standard normal distribution
Example:
[option's delta series across the spot ladder at a particular strike price]
Using the Black-Scholes equation,
[ (LN(1488.05/1490.00) + (0.06-0+0.2145^2/2)*0.0055) / 0.2145*√0.0055 ] from the standard normal distribution.
N(d1) = 0.4785
The below table represents option delta values and prices across the movement in the price of the underlying asset. This can be calculated with the help of the above equation.
Observation-1: Considering an ATM option, the probability of the option landing ITM is 50%, and therefore, the delta of an ATM call option remains close to 0.5 and that of an ATM put option -0.5.
As the price of the underlying asset increases (from ATM to ITM to deep ITM i.e. from $1488.05 to $1498.05 to $1508.05), the delta of the call option also increases (from 0.4785 to 0.6435 to 0.7843). As the option gets further ITM, the probability that the option will land ITM increases, and therefore, the call option's delta also increases. This makes the deep ITM options more attractive as the probability of their getting exercised is high, and therefore, the delta of a deep ITM call option is also high.
As the price of the underlying asset decreases (from ATM to OTM to deep OTM i.e. from $1488.05 to $1478.05 to $1468.05), the delta of the call option also decreases (from 0.4785 to 0.3162 to 0.1825). As the option gets further OTM, the probability that the option will land ITM decreases, and therefore, the call option's delta also decreases. This makes the deep OTM options less attractive as the probability of their getting exercised is low, and therefore, the delta of a deep OTM call option is also low.
Observation-2: Considering the near ATM options (price range of $1458.05 to $1518.05), the option's delta curves are steeper than that of the deep ITM and OTM options.
(expanding the coverage of near ATM options)
This is because of the fact that the near ATM options are more sensitive to the change in the price of the underlying asset as these options have a nearly 50% probability of them getting exercised and a near 50% probability of them getting lapsed. This creates uncertainty in the minds of the traders leading to a higher number of buy-sell positions resulting in higher variability in the option's delta as shown above.
Observation-3: Considering the other options trading deep ITM or OTM has a greater probability of them getting exercised or lapsed, respectively, as a small change in the price of the underlying asset won't be impacting much on the probability, and therefore, the delta value remains reasonably stable.
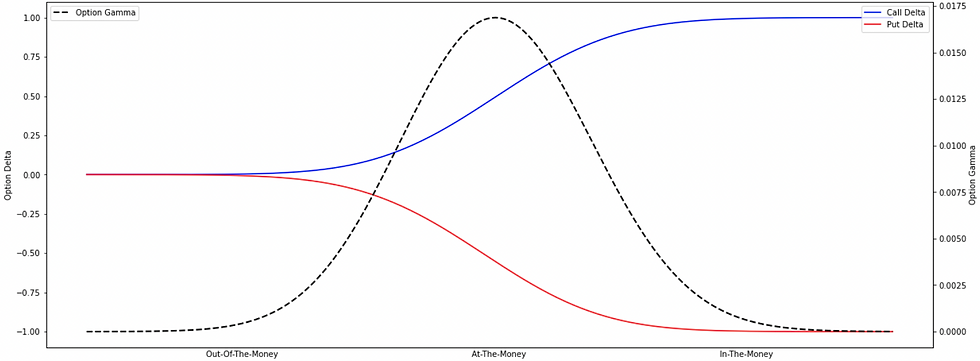
This is the main reason why the option's gamma i.e. the second-order derivative is comparatively higher for near ATM options and lower for ITM and OTM options.
Understanding Delta is key to becoming an Expert in Trading Options
Professional traders are more interested in monitoring the entire options chain having both options prices and their corresponding delta-gamma values across strike prices as it helps them to, (1). estimate any potential change in the underlying price impacting all the positions that they have in the options market. (2). adjust their positions by buying or selling those options.